Coin Change Problems
Problem
- https://leetcode.com/problems/coin-change/
- https://neetcode.io/problems/coin-change
- [Solution] https://www.youtube.com/watch?v=H9bfqozjoqs
Key patterns
- coins array
- infinite supply of coins
- minimum number of coins
For min coins problems, A common, efficient solution to this problem is to use a greedy algorithm. In this situation, you repeatedly select the largest coin that isn’t larger than the remaining amount of change (more info here). However, this doesn’t work for arbitrary combinations of coins (consider 1¢, 6¢, and 10¢ coins and using a greedy algorithm to compute makeChange(12)). Therefore, we will instead focus on a generalized solution.
The user is discussing the "minimum coins" problem and highlighting a key limitation of the greedy algorithm approach. They correctly point out that while a greedy strategy works for standard coin denominations (like US or Euro currency), it fails for arbitrary coin sets. The example given (1¢, 6¢, and 10¢ coins to make 12¢) is a perfect illustration:
-
Greedy approach for 12¢ with {1, 6, 10}:
-
Take 10¢ (remaining: 2¢)
-
Take 1¢ (remaining: 1¢)
-
Take 1¢ (remaining: 0¢)
Total: 3 coins (10¢, 1¢, 1¢)
-
-
Optimal solution for 12¢ with {1, 6, 10}:
-
Take 6¢ (remaining: 6¢)
-
Take 6¢ (remaining: 0¢)
Total: 2 coins (6¢, 6¢)
-
As the user states, the greedy algorithm is not a generalized solution for arbitrary coin denominations. They are therefore shifting the focus to a generalized solution, which typically implies a dynamic programming approach.
The user's statement sets the stage for a discussion or explanation of dynamic programming for the minimum coin change problem.
// Brute force solution. Go through every
// combination of coins that sum up to c to
// find the minimum number
private int[] coins = new int[]{10, 6, 1};
public int makeChange(int c) {
if (c == 0) return 0;
int minCoins = Integer.MAX_VALUE;
// Try removing each coin from the total and
// see how many more coins are required
for (int coin : coins) {
// Skip a coin if it’s value is greater
// than the amount remaining
if (c - coin >= 0) {
int currMinCoins = makeChange(c - coin);
if (currMinCoins < minCoins)
minCoins = currMinCoins;
}
}
// Add back the coin removed recursively
return minCoins + 1;
}
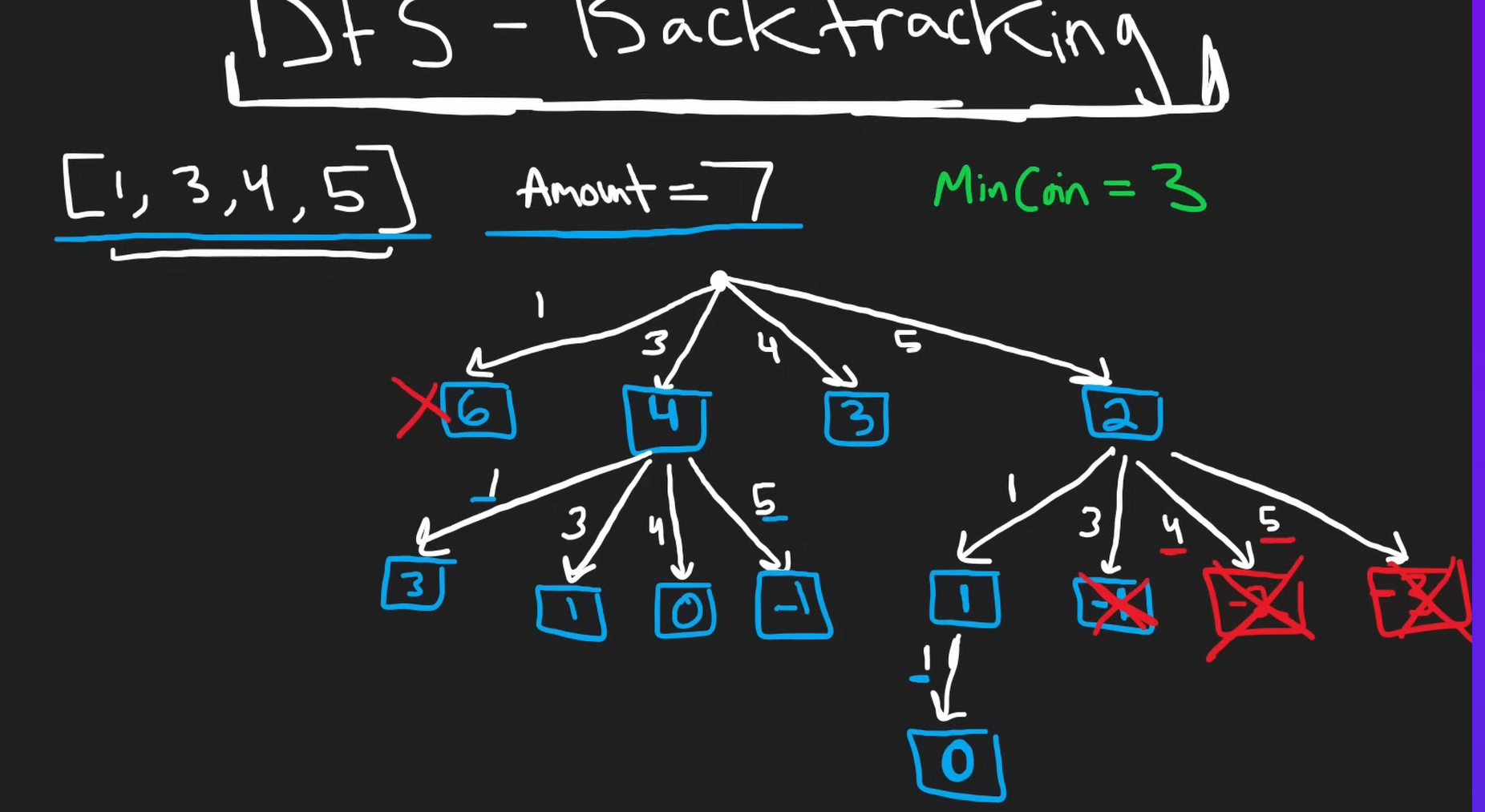
Things to observe
- Plain Greedy won't work - don't start with biggest coin
- Start with DFS and look for 'repeated sub problems'
- This results into top-bottom optimization.
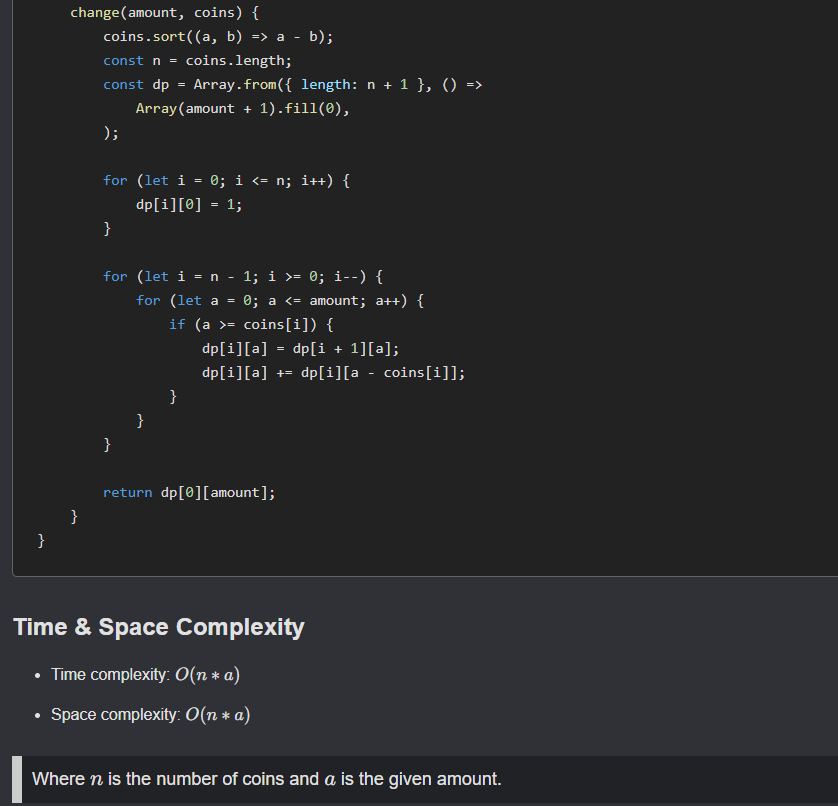
- At this point, It can be also solved as Bottom-up dynamic problem
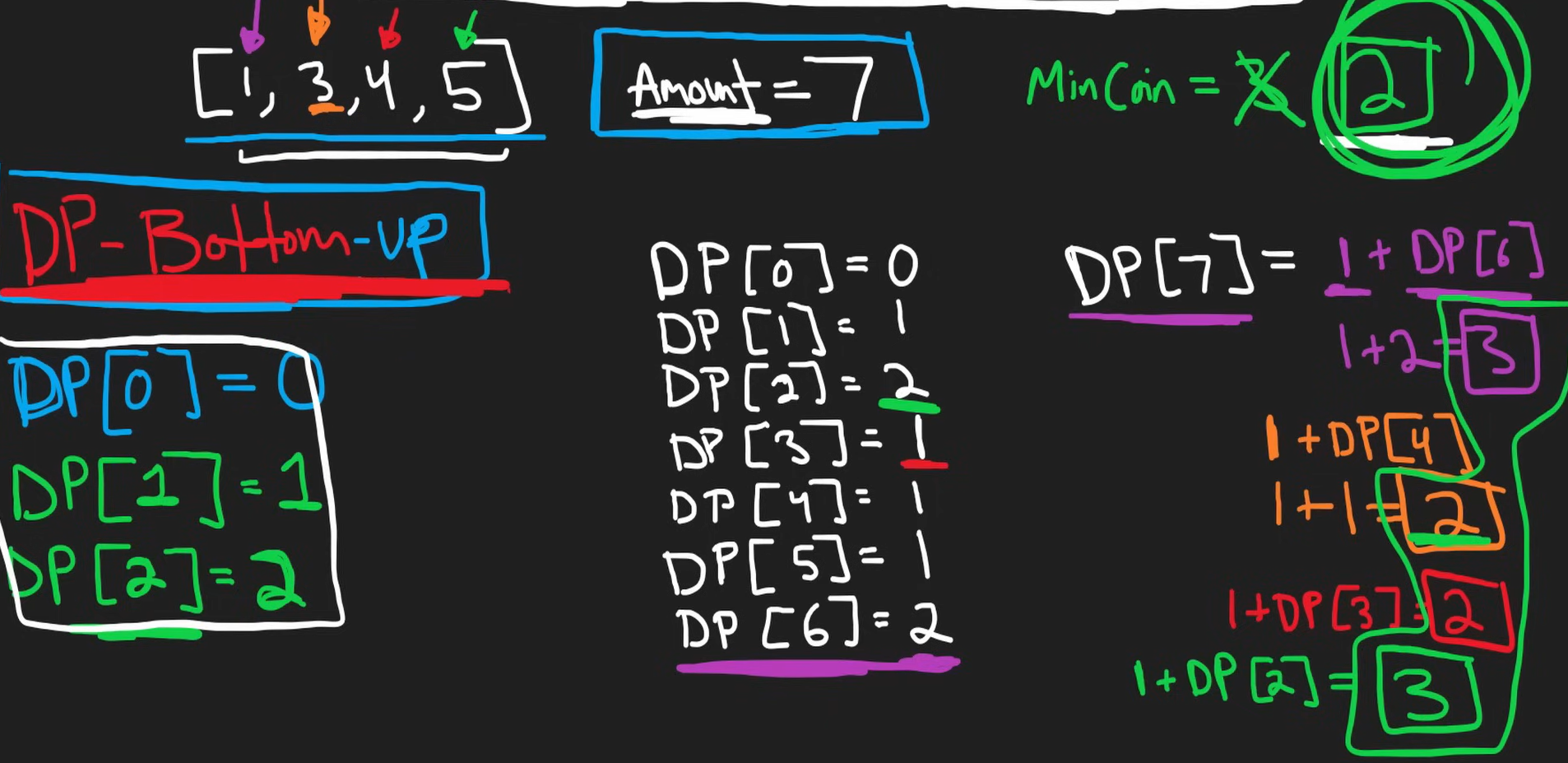
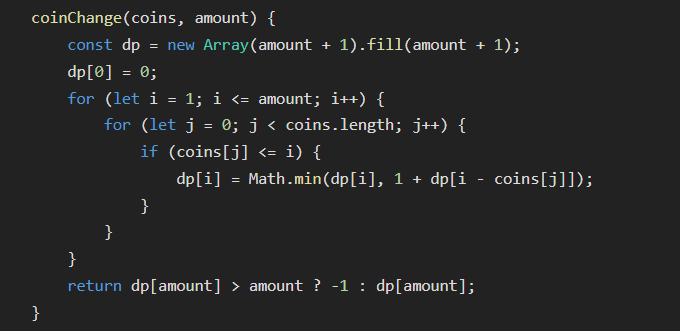
Solution
-
Time complexity: O(n∗t)
-
Space complexity: O(t)
-
initialize a dp array to keep coins needed to form a sum as index
-
dp[0]= 0; -
dp[amount]is question -
initialize this array with a odd/high value like amount+1 so that at last we can check for it
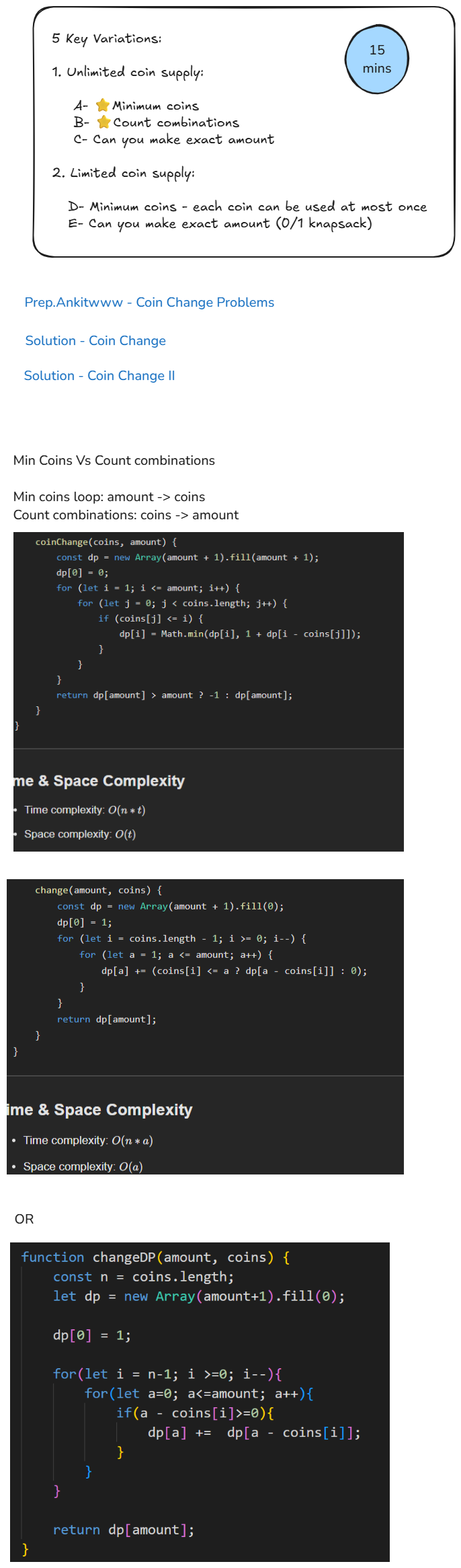
Variations
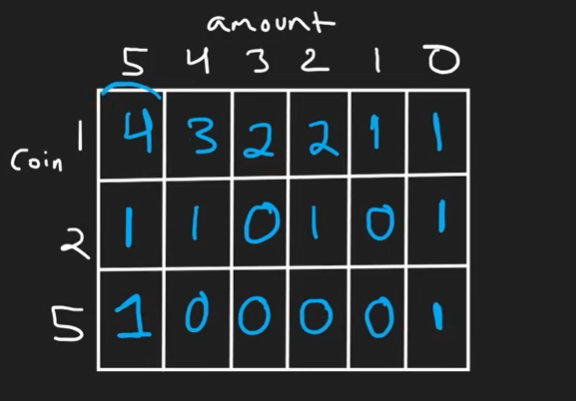
Coin Change 2
- How a
m^nproblem can becomem*nby memoization? - How they avoided duplicate combinations?
- 2D dynamic problem which can be further optimized for memory o(amount)
- dfs(coin, amount)
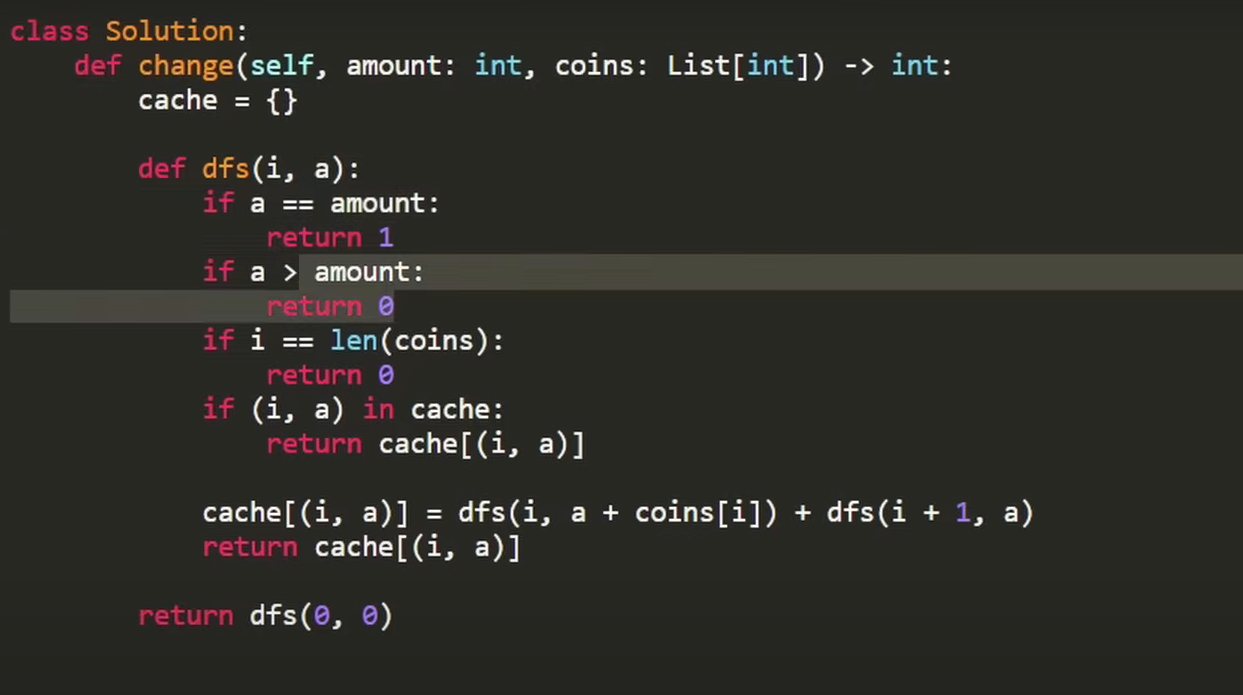
- The magical DP grid