Dynamic Programming - FAST
Three friends: Recursion, memoization and Dynamic Programming (bottom-up/ tabulation)
The FAST method is a formula for turning a recursive algorithm that has repeating subproblems into a bottom-up dynamic programming algorithm.
If you ever encounter a dynamic programming problem in an interview, you should confidently build the recursive solution first, then use this method to shift to dynamic programming.
Dynamic programming is an algorithmic strategy that computes answers to small subproblems, stores those results, and uses them to compute answers to larger and larger subproblems.
The ultimate goal of this process is to improve runtime. Dynamic programming allows you to use more space to take less time.
Most situations where dynamic programming might apply are also problems that can be solved with recursive backtracking.
Dynamic Programming vs Memoization
Many people use these two terms interchangeably, but there is a subtle difference. Memoization is a straightforward addition to the recursive strategy whereby the answer to every computed subproblem is stored for future use when and if that subproblem comes up again. This is still top-down, breaking down the given problem instance into smaller and smaller subproblems.
True dynamic programming is bottom-up. The process starts with the trivial cases, often the base cases in the recursive version, and then combines them to compute answers to successively larger subproblems. This process continues until we reach the answer we’re looking for.
Bottom-up vs Top-down
The important point is that top-down = recursive and bottom-up = iterative
lets review two solutions of Climb stair problem:
A bottom-up approach, also known as tabulation, solves a problem by starting from the smallest subproblems and iteratively building up to the final solution. In this case:
-
Base Cases: The calculation starts with the simplest cases:
dp1 = 1(forn=1) anddp2 = 2(forn=2). -
Iteration: The
forloop then calculates the number of ways to climb fori = 3, 4, 5, ...up ton. -
Building Up: Each new value
dp2is calculated using the previously computed values (dp1and the olddp2). It builds the solution fornfrom the "bottom" (the smallest values) up.
climbStairs(n) {
if (n <= 2) {
return n;
}
let dp1 = 1;
let dp2 = 2;
for (let i = 3; i <= n; i++) {
[dp1, dp2] = [ dp2, dp1 + dp2];
}
return dp2;
}
In contrast, a top-down approach would use recursion to break down the problem from the top (n) and use memoization to store the results of subproblems to avoid re-computation. A top-down solution would look more like this:
const memo = new Map();
function climbStairsTopDown(n) {
if (n <= 2) return n;
if (memo.has(n)) return memo.get(n);
const result = climbStairsTopDown(n - 1) + climbStairsTopDown(n - 2);
memo.set(n, result);
return result;
}
There are four steps in the FAST method:
- First solution
- Analyze the first solution
- Identify the Subproblems
- Turn the solution around
Optimal Substructure
Optimal substructure requires that you can solve a problem
based on the solutions of subproblems. For example, if you
want to calculate the 5th Fibonacci number, it can be solved by
computing fib(5) = fib(4) + fib(3). It is not necessary to
know any more information other than the solutions of those
two subproblems, in order to get the solution.
A useful way to think about optimal substructure is whether a
problem can be easily solved recursively. Recursive solutions
inherently solve a problem by breaking it down into smaller
subproblems. If you can solve a problem recursively, it most
likely has an optimal substructure.
Overlapping Subproblems
Overlapping subproblems means that when you split your
problem into subproblems, you sometimes get the same
subproblem multiple times. With the Fibonacci example, if
we want to compute fib(5), we need to compute fib(4) and
fib(3). However, to compute fib(4), we need to compute fib(3)
again. This is a wasted effort, since we’ve already computed the
value of fib(3).
Dynamic programming relies on overlapping subproblems,
because it uses memory to save the values that have already
been computed to avoid computing them again. The more
overlap there is, the more computational time is saved.
2D Dynamic Problems
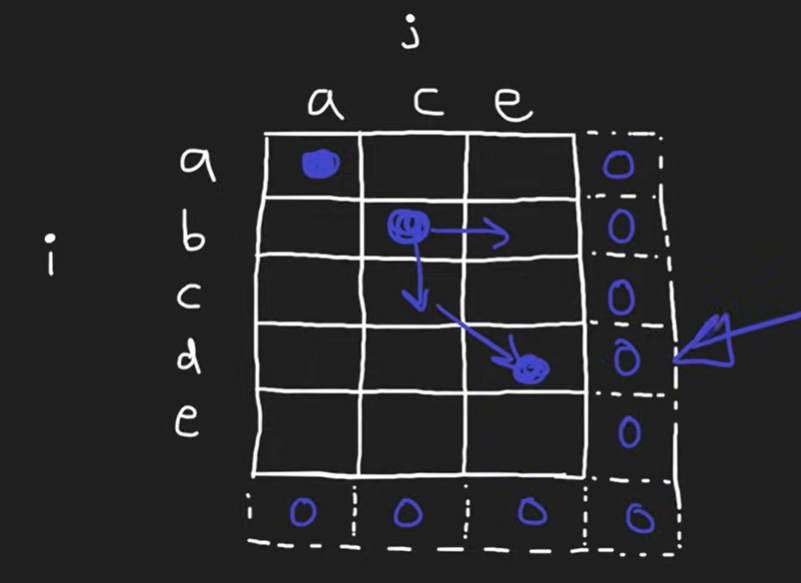
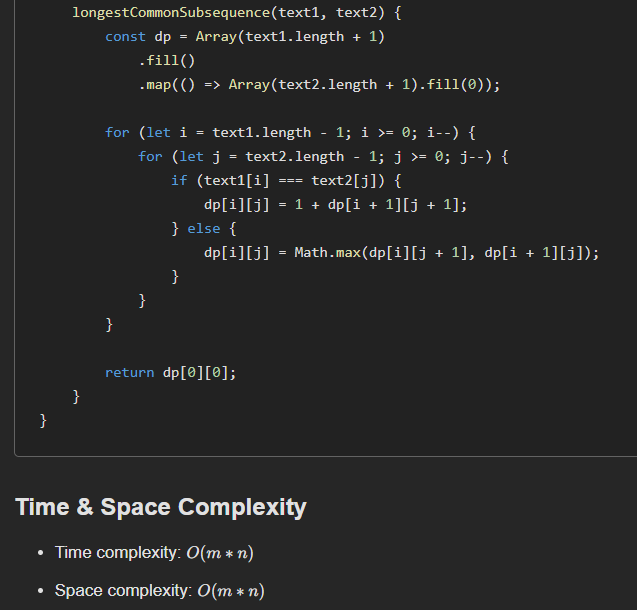
Longest Common Subsequence
Target Sum
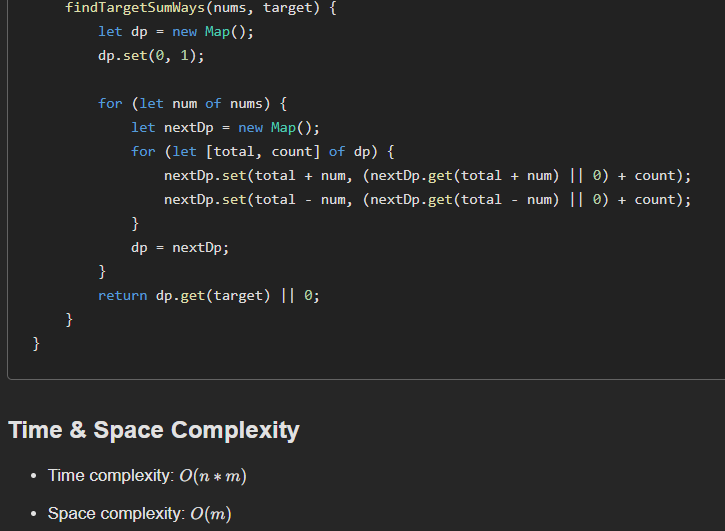
Target sum can be solved DFS + Caching solution in o(n X m) time and space.
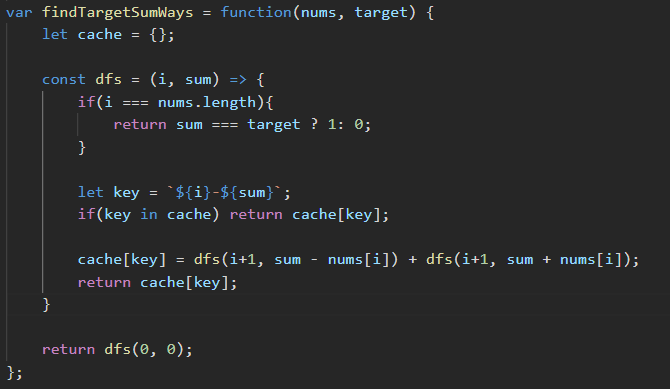
DP solution is having better memory: