Heap

Kth Largest Element in Unsorted Array - Heapify vs insert

-> sorting: nlog(n) & o(1) space
-> Max heap: maximum value on top
- create a max heap by heapifying - O(n)
- No need to do one by one insert as it will take n.log(n)
- pop for k times - k.log(N)
- Total : N + k.log(N)
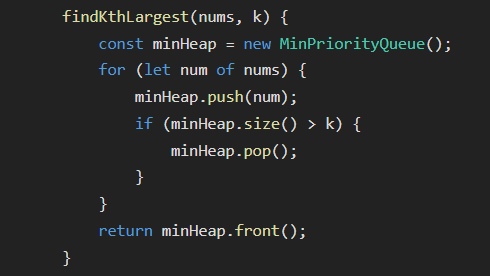
-> Min heap: min value on top
- create a min heap of size k
- first push k elements (one by one) => k.log(k)
- then after for remaining n-k -> pop and then push => (n-k).log(k)
- total (Essentially we push every element in heap) - n.log(k)

Comparison of Approaches

1. Sorting Approach
   • Sort the array and pick the Kth largest element.
   • Time Complexity: O(Nlog⁡N)
   • Space Complexity: O(1) if sorting is done in place.
2. Min Heap Approach
   • Use a min heap (priority queue) of size K.
   • Iterate through the array, maintaining only the top K largest elements.
   • The root of the min heap will be the Kth largest element.
   • Time Complexity: O(Nlog⁡K)
     • Building the heap takes O(Klog⁡K)
     • Inserting N−K elements and maintaining heap property takes O((N−K)log⁡K)
   • Space Complexity: O(K) (since we store only K elements)

Conclusion

• For large N and small K → Min heap is better.
• For small N or if K is close to N → Sorting is fine.
• If modifications to the array are not allowed → Min heap is useful.