Sorting FTW
Sorting algorithms can be broadly classified into two categories:
- Comparison-Based Sorting → These algorithms sort elements by comparing them (e.g., Quick Sort, Merge Sort, Heap Sort).
- Non-Comparison Sorting → These algorithms do not compare elements directly. Instead, they use properties like the digit structure of numbers or frequency counts.
Stable vs Non-stable
A stable sorting algorithm maintains the relative order of equal elements in the sorted output.
✅ Stable Sorting → If two elements have the same value, their original order is preserved in the sorted result.
❌ Unstable Sorting → The original order of equal elements may change.
Use a stable sort when:
- Sorting objects where a second sorting criterion is needed (e.g., sorting by last name, then by first name).
- Sorting lists that were already partially sorted and you want to maintain order.
Key Sorting algos
| Sorting Algorithm | Stable? | Type | Time Complexity (Best / Avg / Worst) | Space Complexity | In-Place? |
|---|---|---|---|---|---|
| Merge Sort | ✅ Yes | Comparison | O(n log n) / O(n log n) / O(n log n) | O(n) | ❌ No |
| Quick Sort | ❌ No | Comparison | O(n log n) / O(n log n) / O(n²) - if arr is already sorted | O(log n) (due to recursion) | ✅ Yes |
| Heap Sort | ❌ No | Comparison | O(n log n) / O(n log n) / O(n log n) | O(1) | ✅ Yes |
| Bubble Sort | ✅ Yes | Comparison | O(n) / O(n²) / O(n²) | O(1) | ✅ Yes |
| Insertion Sort | ✅ Yes | Comparison | O(n) / O(n²) / O(n²) | O(1) | ✅ Yes |
| Counting Sort | ✅ Yes | Non-Comparison | O(n + k) / O(n + k) / O(n + k) | O(k) | ❌ No |
| Radix Sort | ✅ Yes | Non-Comparison | O(nk) / O(nk) / O(nk) | O(n + k) | ❌ No |
💡 Key Observations
✔️ In-Place Sorting (✅ Yes): Uses O(1) or O(log n) extra space, modifying the original array (Quick Sort, Heap Sort, Bubble Sort, Insertion Sort).
✔️ Not In-Place (❌ No): Requires additional memory for merging or auxiliary structures (Merge Sort, Counting Sort, Radix Sort).
✔️ Merge Sort is stable but not in-place because it requires extra space for merging.
✔️ Quick Sort is in-place but not stable because swapping elements may change their relative order.
✔️ Counting and Radix Sort are stable but not in-place since they use extra memory to sort.
Further Notes
For FAANG interviews, you should focus on the following sorting algorithms, categorized by importance:
🔥 Must-Know Sorting Algorithms (Used Frequently in Interviews)
1️⃣ Quick Sort (Divide and Conquer)
- Time Complexity: O(n log n) average, O(n²) worst-case (when poorly partitioned)
- Space Complexity: O(log n) (due to recursive calls)
- Best for: General-purpose sorting, often used in practical applications.
- Key Concept: Picks a pivot, partitions elements around it, and recursively sorts.
2️⃣ Merge Sort (Divide and Conquer)
- Time Complexity: O(n log n) (always)
- Space Complexity: O(n)
- Best for: Sorting linked lists, stable sorting needs.
- Key Concept: Splits array into halves, sorts them, then merges them.
3️⃣ Heap Sort (Priority Queue-Based Sorting)
- Time Complexity: O(n log n) (always)
- Space Complexity: O(1) (in-place sorting)
- Best for: Situations requiring O(1) extra space with guaranteed O(n log n) sorting.
- Key Concept: Uses a binary heap to sort elements by repeatedly extracting min/max.
⚡ Important to Know (Less Common in Interviews but Useful)
4️⃣ Counting Sort (Non-Comparison Based)
- Time Complexity: O(n + k) (where k = range of numbers)
- Space Complexity: O(k)
- Best for: Small integer ranges (e.g., sorting ages, exam scores).
- Key Concept: Uses frequency counting instead of comparisons.
5️⃣ Radix Sort (Non-Comparison Based)
- Time Complexity: O(nk) (where k = number of digits in the max number)
- Space Complexity: O(n + k)
- Best for: Sorting large numbers efficiently.
- Key Concept: Sorts numbers digit by digit using Counting Sort as a subroutine.
🎯 Basic Sorting Algorithms (Not Used in Interviews but Good for Understanding Basics)
6️⃣ Bubble Sort
- Time Complexity: O(n²)
- Space Complexity: O(1)
- Best for: Teaching sorting but not used in practice.
- Key Concept: Repeatedly swaps adjacent elements if they are in the wrong order.
7️⃣ Selection Sort
- Time Complexity: O(n²)
- Space Complexity: O(1)
- Best for: Small datasets, theoretical understanding.
- Key Concept: Selects the smallest element and places it at the beginning.
8️⃣ Insertion Sort
- Time Complexity: O(n²) (O(n) for nearly sorted input)
- Space Complexity: O(1)
- Best for: Small datasets, nearly sorted lists.
- Key Concept: Builds sorted order one element at a time by inserting in the right position.
📌 Which Sorting Algorithms Should You Master for Interviews?
- Quick Sort 🏆 (Most commonly asked in interviews)
- Merge Sort 💡 (Guaranteed O(n log n), useful in recursion-based problems)
- Heap Sort ⚙️ (Efficient in-place sorting)
- Counting Sort & Radix Sort 🚀 (For non-comparison sorting problems)
JavaScript and sorting algo
In JavaScript (specifically in V8, which powers Node.js and Chrome), the built-in .sort() method uses different sorting algorithms based on the data type and length of the array:
- TimSort (a hybrid of Merge Sort and Insertion Sort)
- Used for arrays of numbers and strings in most cases.
- TimSort is optimized for partially sorted data, making it efficient in real-world scenarios.
- Insertion Sort
- Used for small arrays (length ≤ 10) because it has low overhead and is fast for small datasets.
How it works in V8:
- For small arrays (
<= 10elements), Insertion Sort is used because of its simplicity and low overhead. - For larger arrays, TimSort is used, which adapts to the structure of the data to improve efficiency.
Time Complexity:
- Best Case (already sorted data): O(n)
- Average Case: O(n log n)
- Worst Case: O(n log n)
Learning
Recursive and D&C
-
Merge Sort
- not in place - but stable - need extra space though for merging O(n)
- code
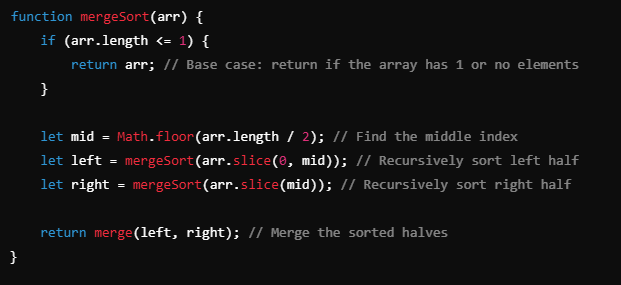
and here is merge function
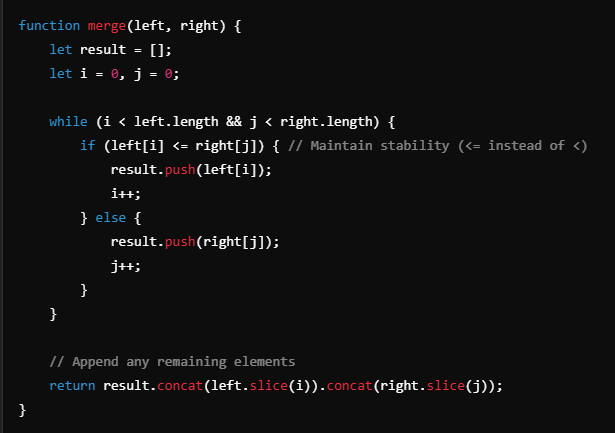
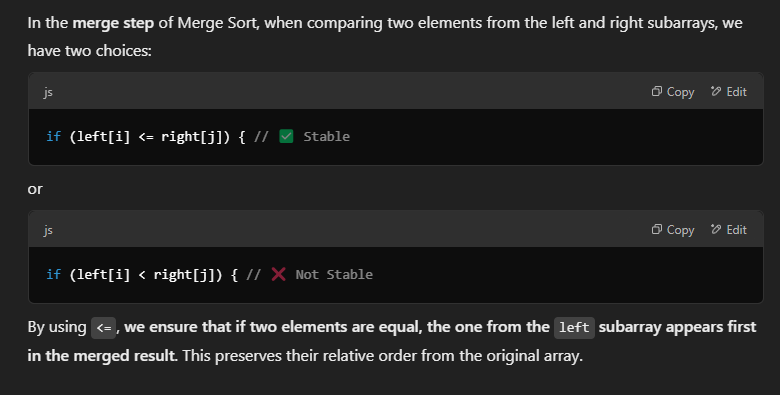
- Notice stability
- NeetCode - https://www.youtube.com/watch?v=MsYZSinhuFo
-
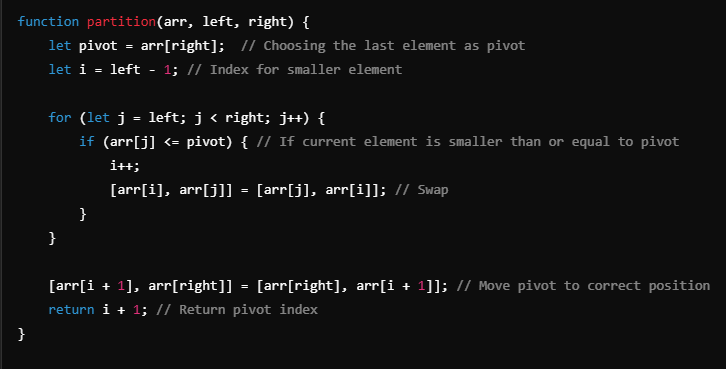
Quick sort
-
In place - but not stable due to swapping
-
still need o(logn) space due to recursion
-
Mantra - "pivot"
-
pick a pivot and partition around pivot
-
Now you got two partitions - sort them recursively
-
notice that signatures of main and partition are almost same!
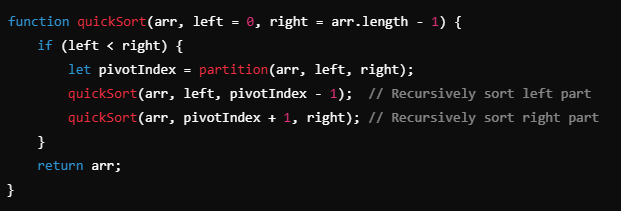
And here is partition function which returns the pivot Index
- Need two pointer i and j
- i is going to be index of smaller element
- eventually, i +1 is going to be pivot final position
-